工作之一,任何 元对称多项式,都可以用这
元对称多项式,都可以用这 个以原来不定元组成的基本对称多项式,唯一地以多项式来表示。
个以原来不定元组成的基本对称多项式,唯一地以多项式来表示。
 元对称多项式,都可以用这
元对称多项式,都可以用这 个以原来不定元组成的基本对称多项式,唯一地以多项式来表示。
个以原来不定元组成的基本对称多项式,唯一地以多项式来表示。
例如当 ,有2个基本对称多项式
,有2个基本对称多项式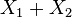 和
和 。第一个例子中的多项式可以写成
。第一个例子中的多项式可以写成
 ,有2个基本对称多项式
,有2个基本对称多项式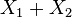 和
和 。第一个例子中的多项式可以写成
。第一个例子中的多项式可以写成 。
。
这个定理,后来被应用到伽罗华的对称群理论中,也就是说,保持韦达定理的不变的对称变换群,实际上是作用在几个初等多项式之上的。
工作之二,是牛顿解释了丢番图《算术》一书中,所做的一个x=3y-1的奇怪变换,就是椭圆曲线在那点的切线方程。后来人们意识到,在椭圆曲线上通过有理点的直线,这直线和椭圆曲线的交点都是有理数,这是一个伟大的成就。
椭圆曲线上的有理点构成的群结构,为后来解决费马大定理铺设了道路。
没有评论:
发表评论