貌似WinXP还是无限经典,我也一直还在用,不知道哪天才会放弃。
这次遇见的问题,也许也有XP爱好者也遇得见,记下点文字备忘。
----------------------- 单调的分割线 ----------------------
家里台式机接无线USB网卡 TL-WN821N 之前一直都是好好的,今天接上去,竟然提示“区域中找不到无线网络”。
下面是解决这问题的简单过程......
这次遇见的问题,也许也有XP爱好者也遇得见,记下点文字备忘。
----------------------- 单调的分割线 ----------------------
家里台式机接无线USB网卡 TL-WN821N 之前一直都是好好的,今天接上去,竟然提示“区域中找不到无线网络”。
下面是解决这问题的简单过程......
据资料说是 WinXP 的 “Wireless Zero Configuration” 服务依赖于“Eventlog”服务;
于是点开始 -> 运行“services.msc”,查看 "Eventlog" 服务发现已经被停止使用了,于是启动 "Eventlog" 服务(记得设置为自动启动方式啊) 再查看 “Wireless Zero Configuration” 服务是启动的,这时候以为万事大吉了,再去刷新网路连接,还是提示“区域中找不到无线网络”。没法啊,接着双击 “Wireless Zero Configuration” 项,弹出设置窗口,此时点击“依存关系”,正常为下面图,应该包含 "Event Log" 项:
于是点开始 -> 运行“services.msc”,查看 "Eventlog" 服务发现已经被停止使用了,于是启动 "Eventlog" 服务(记得设置为自动启动方式啊) 再查看 “Wireless Zero Configuration” 服务是启动的,这时候以为万事大吉了,再去刷新网路连接,还是提示“区域中找不到无线网络”。没法啊,接着双击 “Wireless Zero Configuration” 项,弹出设置窗口,此时点击“依存关系”,正常为下面图,应该包含 "Event Log" 项:
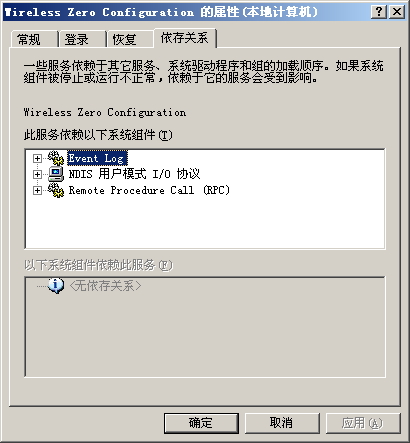
如果你发现 “Wireless Zero Configuration” 的依存关系有"Event Log" 这项,下面的文字请你直接忽略,你的情况不是本文所能解决的了。
如果没有"Event Log" 项,必须手工通过注册表加入依存关系了:
点开始 -> 运行 “regedit” 进入注册表,依次进入下面项:[HKEY_LOCAL_MACHINE\SYSTEM\CurrentControlSet\Services]
找到 “WZCSVC” 项目, 双击它的值项“DependOnService”,在值设置窗口输入一行:“Eventlog” (不含引号),点击确定后保存。
点开始 -> 运行 “regedit” 进入注册表,依次进入下面项:[HKEY_LOCAL_MACHINE\SYSTEM\CurrentControlSet\Services]
找到 “WZCSVC” 项目, 双击它的值项“DependOnService”,在值设置窗口输入一行:“Eventlog” (不含引号),点击确定后保存。
正常值有下面三项:
RpcSs
Ndisuio
Eventlog
RpcSs
Ndisuio
Eventlog
加入 Eventlog 依存关系后,必须重新启动 “Wireless Zero Configuration” 服务,好了,再去刷新无线网络列表,终于刷到了各个无线点名称了。
另外很重要的一点是:请确保 Eventlog 服务 是启动状态!(请检查它的状态,如果不是自动运行,请设置为自动,然后启动它)
如果设置 Eventlog 服务启动后,还刷不到网络,这时候可以试着重新启动一下XP操作系统,也许你有惊喜了。

 ,有2个基本对称多项式
,有2个基本对称多项式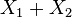 和
和 。第一个例子中的多项式可以写成
。第一个例子中的多项式可以写成 。
。
 × r =
× r =